
Hence, largest integer value of \(a\) is \(48\). What is the largest integer value of \(a\) for which Professor Caesar’s algorithm would be asymptotically faster than Strassen’s algorithm?Īssymptotic running time for Strassen’s algorithm is \(S(n) = \Theta(n^\). If his algorithm creates \(a\) subproblems, then the recurrence for the running time \(T(n)\) becomes \(T(n) = aT(n/4) + \Theta(n^2)\). He needs to determine how many subproblems his algorithm has to create in order to beat Strassen’s algorithm. His algorithm will use the divide-and-conquer method, dividing each matrix into pieces of size \(n/4 \times n/4\), and the divide and combine steps together will take \(\Theta(n^2)\) time.
take upper left corner of the result matrix based on dimensions of operands.


To get back to your rectangular result, you would just crop the result, i.e. Dynamic Programming Vs Greedy Algorithm 1 Answer Sorted by: 2 The result matrix is going to contain zeros on all items that were 'added' to operand matrices.Divide and Conquer Vs Dynamic Programming.S 7 = (A 12 – A 22) x (B 21 + B 22) Some Popular Problems Solved using Divide and ConquerĪdditional Reading: Intuitive explanation of the Strassen matrix multiplication I am having trouble getting divide and conquer matrix multiplication to work.
#Matrix multiplication divide and conquer algorithm code#
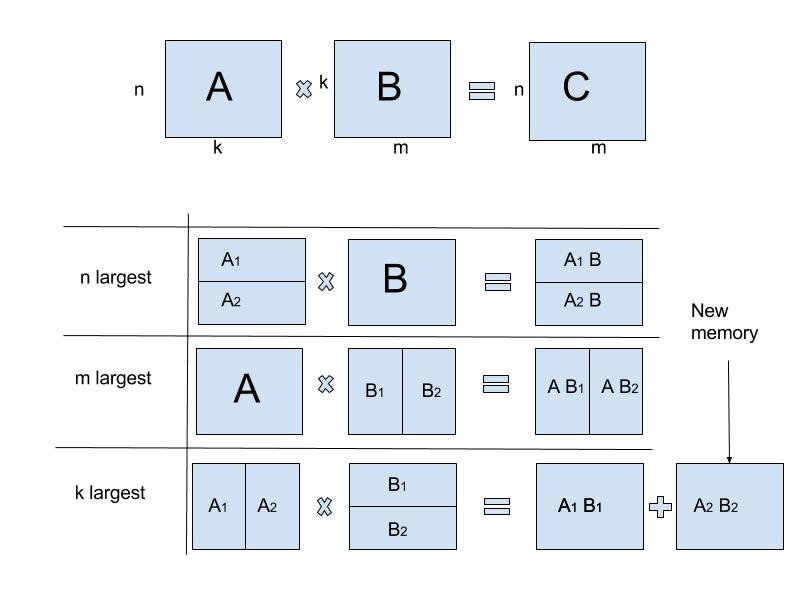
Problem: Multiply given two matrices A and B using Strassen’s approach, where Strassen algorithm for matrix multiplication (divide and conquer) - Inside code Inside code 22K subscribers Subscribe 27K views 1 year ago Algorithms Source code. Example of Matrix Multiplication using Divide and Conquer Approach The difference between running time becomes significant when n is large. Thus, running time of Strassen’s matrix multiplication algorithm O(n 2.81), which is less than cubic order of traditional approach. By substituting n = (n / 2) in above equation, Let us find the solution using the iterative approach. Two matrices of size 1 x 1 needs only one multiplication, so the base case would be, T (1) = 1. Recurrence equation for Strassen’s approach is given as, In short, to solve the problem of size n, Strassen’s approach creates seven problems of size (n – 2). Whereas Strassen’s approach performs seven multiplications on the problem of size 1 x 1, which in turn finds the multiplication of 2 x 2 matrices using addition. It is faster than the standard matrix multiplication algorithm for large matrices, with a better asymptotic complexity, although the naive algorithm is often better for smaller matrices. The conventional approach performs eight multiplications to multiply two matrices of size 2 x 2. In linear algebra, the Strassen algorithm, named after Volker Strassen, is an algorithm for matrix multiplication. STRESSEN_MAT_MUL (A + 3 * (n/4), B + 3 * (n/4), C + 3 * (n/4), n/4)Įnd Complexity Analysis of Matrix Multiplication using Divide and Conquer approach Naïve Method First, we will discuss naïve method and its complexity. We want to calculate the resultant matrix Z by multiplying X and Y. Problem Statement Let us consider two matrices X and Y. STRESSEN_MAT_MUL (A + (n/4), B + 3 * (n/4), C + (n/4), n/4) In this chapter, first we will discuss the general method of matrix multiplication and later we will discuss Strassen’s matrix multiplication algorithm.

STRESSEN_MAT_MUL (A + (n/4), B + 2 * (n/4), C, n/4) Divide and Conquer Matrix Multiplication Ask Question Asked 12 years, 3 months ago Modified 10 years, 8 months ago Viewed 17k times 9 I am having trouble getting divide and conquer matrix multiplication to work. Algorithm Algorithm STRESSEN_MAT_MUL (int *A, int *B, int *C, int n) Similarly we can derive all C ij for strassen’s matrix multiplication. This is same as C 12 derived using conventional approach. Let us check if it is same as the conventional approach.


 0 kommentar(er)
0 kommentar(er)
